Binary Addition using Half and Full Adders within TypeScript

Recently, I watched an interesting talk about Binary Addition in the TypeScript Type System. I thought it would be fascinating to explore this concept in more depth. I wanted to pay close attention to how I could leverage the TypeScript type system to help ensure validity in the final implementation.

The Bit

Starting from basic principles and working our way up, we define the concept of a Bit and a fixed tuple of Bits using Recursive Conditional Types which will be available in TypeScript 4.1.

type Bit = 0 | 1;
type Bits<N extends number> = N extends N ? (number extends N ? Bit[] : _Bits<N, []>) : never;
type _Bits<N extends number, R extends Bit[]> = R["length"] extends N ? R : _Bits<N, [Bit, ...R]>;

From here, we create a simple factory function which, based on the desired bit width size, pads out a supplied Partial type with trailing zeros. For this exercise, we will be storing the bits in Least Significant Bit order.

type PartialBits<N extends number> = Partial<Bits<N>>;

const Bits = <N extends number>(size: N) => (bits: PartialBits<N>): Bits<N> => {
  let result = Array<Bit>(size) as Bits<N>;

  for (let i = 0; i < size; i++) {
    result[i] = bits[i] || 0;
  }

  return result;
};

const Int8 = Bits(8);
const Int16 = Bits(16);

In doing this, we are now leveraging the type system to ensure that any supplied bits do not exceed the allocated representation width. This is highlighted in the examples below.

Int8([1, 0, 1]); // valid
Int8([1, 0, 0, 1, 1, 0, 1, 0, 1]); // invalid
Int16([1, 0, 0, 1, 1, 0, 1, 0, 1]); // valid

The Logic Gates

So, to perform the final addition, we need to provide the tooling around being able to construct logic gates based on supplied bits. We are able to achieve this using the approach laid out below.

const and = (a: Bit, b: Bit): Bit => (a === 1 && b === 1 ? 1 : 0);
const or = (a: Bit, b: Bit): Bit => (a === 1 || b === 1 ? 1 : 0);
const invert = (a: Bit): Bit => (a ? 0 : 1);
const nand = (a: Bit, b: Bit): Bit => invert(and(a, b));
const nor = (a: Bit, b: Bit): Bit => invert(or(a, b));
const xor = (a: Bit, b: Bit): Bit => and(or(a, b), nand(a, b));

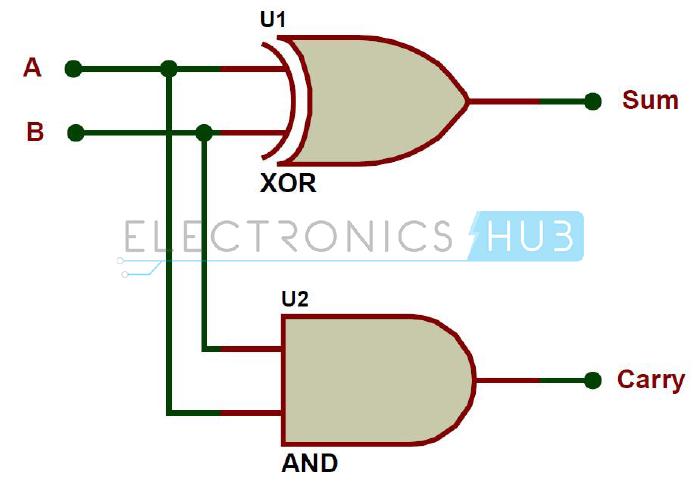
The Half Adder

The Half Adder is used to add two single bits A and B together, resulting in sum and carry outputs. We can build such a circuit using the following three approaches – the simplest of which is shown first, comprising a single XOR and AND gate.

type Addition = {
  sum: Bit;
  carry: Bit;
};

type HalfAdder = (a: Bit, b: Bit) => Addition;

Simplest Half-Adder

const halfAdder: HalfAdder = (a, b) => ({
  sum: xor(a, b),
  carry: and(a, b),
});

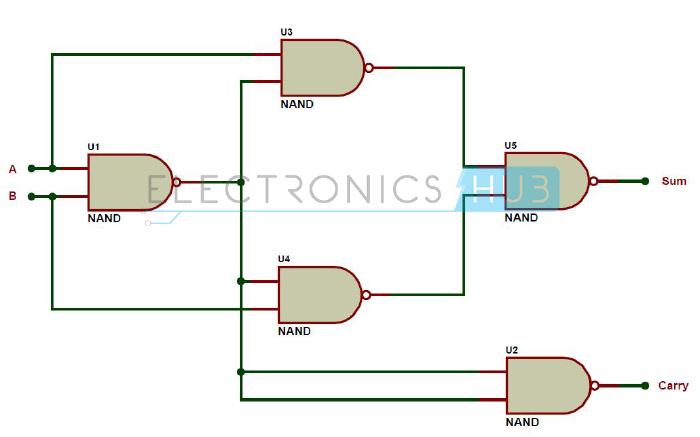
Half-Adder using only NAND Gates

const halfAdderUsingNand: HalfAdder = (a, b) => {
  const ab = nand(a, b);
  return {
    sum: nand(nand(ab, a), nand(ab, b)),
    carry: nand(ab, ab),
  };
};

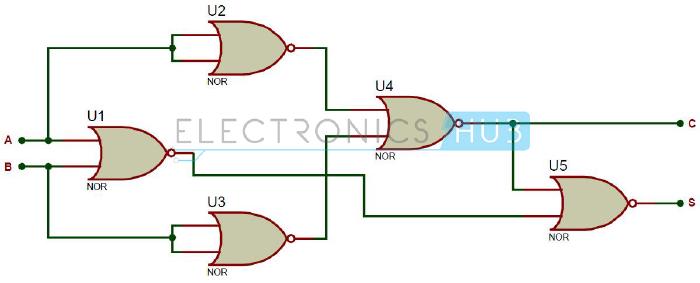
Half-Adder using only NOR Gates

const halfAdderUsingNor: HalfAdder = (a, b) => {
  const carry = nor(nor(a, a), nor(b, b));
  return {
    sum: nor(carry, nor(a, b)),
    carry,
  };
};

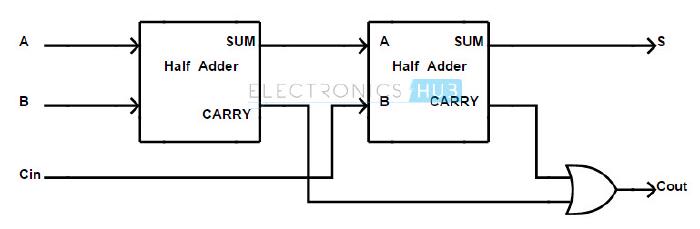
The Full Adder

On its own, a half adder is unable to perform the binary addition we hope to achieve. To overcome this, we can use a Full Adder which is able to handle a subsequent third bit within the input – this being the carry from a previous operation. This adder can be constructed by using two half adders as follows.

type FullAdder = (a: Bit, b: Bit, c: Bit) => Addition;

const fullAdder = (halfAdder: HalfAdder): FullAdder => (a, b, c) => {
  const ab = halfAdder(a, b);
  const abc = halfAdder(ab.sum, c);
  return {
    sum: abc.sum,
    carry: or(ab.carry, abc.carry),
  };
};

Binary Addition

With this tooling in place, we can then construct an addition function. Based on a bit result width size, we supply partials of this bit width and in turn use the full adder to calculate the final result. Leveraging the type system, we are able to ensure that we do not permit inputs that exceed the allocated return type.

const add = (fullAdder: FullAdder) => <N extends number>(size: N) => (
  a: PartialBits<N>,
  b: PartialBits<N>
): Bits<N> => {
  let carry: Bit = 0;
  let result = Array<Bit>(size) as Bits<N>;

  for (let i = 0; i < size; i++) {
    ({ sum: result[i], carry } = fullAdder(a[i] || 0, b[i] || 0, carry));
  }

  return result;
};

Finally, we can test out this implementation as follows.

const addInt8 = add(fullAdder(halfAdder))(8);
const addInt16 = add(fullAdder(halfAdderUsingNand))(16);

addInt8(Int8([1, 0, 1, 1]), Int8([1, 0, 1])); // 01001000
addInt8(Int16([1, 0, 1, 1, 1, 1, 1, 1, 1]), Int8([1, 1, 1, 1])); // invalid
addInt16(Int16([1, 0, 1, 1, 1, 1, 1, 1, 1]), Int8([1, 1, 1, 1])); // 0011000001000000

Notice the type system again helping to enforce width rules with regard to bits in the second example. If you are interested in experimenting with the demonstration, you can visit this TypeScript playground.