The Mystery Calculator in ClojureScript and Reagent

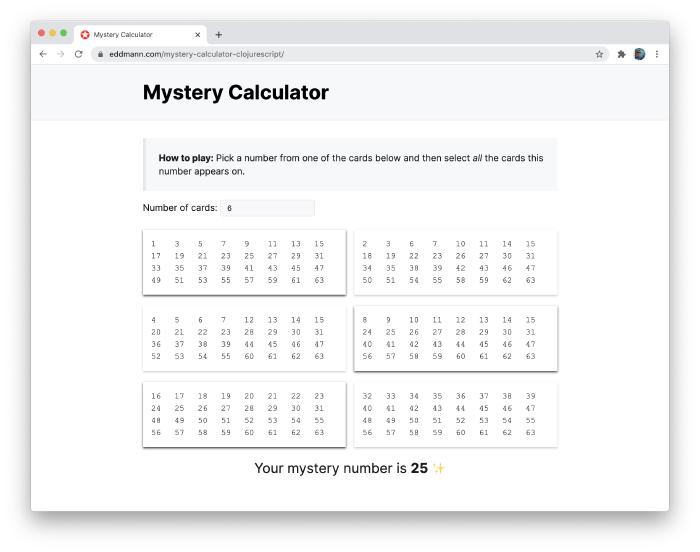
The Mystery Calculator is a commonly found Christmas cracker gift, which uses a neat powers of two (binary) addition trick to fool the spectator. I thought it would be interesting to create a small web application in ClojureScript and Reagent, which provided the ability to generate a selection of these cards and perform the trick.

You can generate a selection of these mystery cards and perform the trick yourself by visiting here, the source-code is also availble on GitHub.

The magic trick is performed as follows:

The complete set consists of N cards, printed with a series of numbers, show all the cards to a friend and ask him or her to select-one number from any one card. Show the other N-1 cards to your friend asking him or her to say whether the number appears on these cards. Take all the cards on which your friend says the number appears, add together the top left hand corner number of each card and the total is the number your friend selected.

How it works?

You may notice that all the card numbers that are chosen can be written in terms of powers of two. Upon closer inspection, you may also see that each number can be written in terms of a subset (or all) of the numbers present in the top-left hand corner of each of the cards.

I found it easier to visualise this by replacing the decimal number represenation with binary. If we number all the available cards (1 to N), you will see that each number on that given card has that positions bit set to 1. This means that we can calculate the mystery number by performing a binary AND operation on the top-left hand corners number for all cards which include the chosen number.

For eample, say I have picked the mystery number 28 (11100 in binary). That number appears on cards 3, 4 and 5 in a convential 6 card setup. The top-left hand corner numbers for these cards are 4 (00100), 8 (01000) and 16 (10000). If we perform the binary AND operation on these numbers we produce the chosen mystery number 28 (11100). This works for any number chosen from the given cards.

Building the Mystery Calculator

Now we are familiar with how it works, we can start by building the functionality which produces these crafted cards based on a desired card count.

(defn- generate-cards [num-of-cards]
  (reduce
    (fn [cards number]
      (map-indexed
        #(if (bit-test number %1) (conj %2 number) %2)
        cards))
    (repeat num-of-cards (vector))
    (range 1 (Math/pow 2 num-of-cards))))

Using a Lisp we are able to succinctly express how a card is formed. First, we produce an exclusive range of all the sequential numbers up-to two to the power of the card count. For each number and card we check to see if the given numbers bit is set to 1 at that cards position. For example, for the first card we would check the first bit, the second card the second bit etc. In doing this reducation we eventually construct all the desired cards with the specifically placed numbers.

Now that we can generate these cards, we next want to present them to the user. To do this I decided to explore using Reagent, which provides an efficient way to create React components using ClojureScript.

(defn- display-cards [chosen-cards cards]
  (let [toggle-choice #((if (contains? %1 %2) disj conj) %1 %2)]
    [:div.cards
      (doall
        (for [card cards]
          ^{:key card}
          [:div {:class ["card" (when (contains? @chosen-cards (first card)) "chosen")]
                 :on-click #(swap! chosen-cards toggle-choice (first card))}
            (map (fn [num] ^{:key num} [:span num]) card)]))]))

Passing in the generated cards from the previous function and a state atom which includes the users selection, we can present these for React to render using Hiccup. If the user clicks on a card, we will toggle the presence of the cards top-left hand corners number within the chosen-cards state atom.

Finally, we can wire up the application, declaring the two state atoms with default values and displaying the mystery number if a card has been selected.

(defn- clamp [x min max]
  (if (< x min) min (if (> x max) max x)))

(defn- app []
  (let [num-of-cards (r/atom 6)
        chosen-cards (r/atom #{})]
    (fn []
      [:div
        [:p
          "Number of cards: "
          [:input {:type "number"
                   :value @num-of-cards
                   :on-change #(reset! num-of-cards (-> % .-target .-value (clamp 4 7)))}]]
        (display-cards chosen-cards (generate-cards @num-of-cards))
        (let [mystery-number (reduce + @chosen-cards)]
          (when (pos? mystery-number)
            [:p.number "Your mystery number is " [:strong mystery-number] " ✨"]))])))

(defn ^:export init []
  (reagent.dom/render [app] (.getElementById js/document "app")))

We include a clamp function which is not present in the ClojureScript core, this provides us with the ability to restrict how many cards can be generated as this can be an expensive Browser operation.

Deployment

To ease deployment and hosting I decided to leverage GitHub Actions and GitHub Pages. Upon a successful Git push, using the provided Makefile and Docker-setup, we first compile the application and subsequently release the artifact to the gh-pages branch. This branch is then used to host the web application made available here.

name: Release

on:
  push:
    branches:
      - master

jobs:
  release:
    runs-on: ubuntu-latest
    steps:
      - uses: actions/checkout@v2
      - run: make release
      - uses: JamesIves/github-pages-deploy-action@releases/v3
        with:
          ACCESS_TOKEN: ${{ secrets.ACCESS_TOKEN }}
          BRANCH: gh-pages
          FOLDER: public